A friend sent me a link to an online kerning game, and I think I might have found my true calling, lulz. I guess my sphere of OCDity extends to include the spacing of letters, even though I’m not a visual person. Arranging and organizing images I can see before me = system running, conceptualizing or manipulating visualizations = system overload. Like I’m truly in awe of people who are good with maps, people who know which direction they’re traveling when they make turns without having to pause and think and confuse themselves in the process.
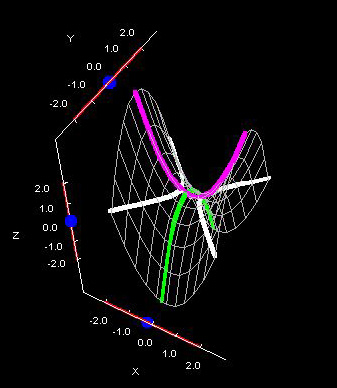
To segue into math, hyperbolic paraboloids are pretty trippy quadratic surfaces. I know what a hyperbolic paraboloid looks like and I can graph one,1 but mentally rotating it (interchanging x, y, and z variables), visualizing traces in various coordinates planes, changing the coefficients, shifting the vertex or attempting to extend 2-D conics in 3-D space, results in the aforementioned system overload crashes.
Hyperbolic Paraboloid Rotation
Hyperbolic Paraboloid Flipping: c > 0, c < 0
Critical Point: Saddle Point (Neither Relative Maxima Nor Relative Minima)
Vertical traces (cross sections) are parabolas; horizontal traces are hyperbolas.

Did You Know?
Saddles and pringles are hyperbolic paraboloids.
Notes
1 Well, admittedly by lazily renaming the x, y, z-axes, yes.
Sources